|
מתי מטיל אלוהים את הקוביות (ב') | 1178 |  |
||||||||
 |
|
 |
|||||||||
 |
פרסומים אחרונים במדור "מדע"
|
| הצג את כל התגובות | הסתר את כל התגובות |
 |
|
 |
||
|
||||
 |
השבירה בלוקליות של המערכת היא בעצם העברת של מידע ממקום אחד לשני באפס זמן. אם ביצענו ניסוי כזה ונתנו ך2 אלקטרוניםפ צמודי ספין לנוע במרחב, כך שיש מרחק משמעותי ביניהם, אז ברגע שנמדוד ספיןשל אלקטרון בצד אחד, הוא יקבע את הספין של האלקטרון השני באופן מידי,(שבירת הלוקאליות) וכך נפתחת אפשרות, שאכן נבחנת בימים אלה, לטלפורטציה - העברת מידע בזמן אפס, ללא תלות במהירות האור. |
 |
 |
 |
|
 |
||
|
||||
 |
טלפורטציה לא מסוגלת להעביר שום מידע באפס זמן. היא כן מסוגלת להעביר מידע רב באמצעות מספר קטן של Qubits כלומר של אלקטרונים או פוטונים במצב קוונטי ידוע. גם בניסוי המתואר במאמר אין אפשרות להעביר מידע בין שתי נקודות המדידה באפס זמן. לכל היותר אתה יודע מה נמדד בצד השני, אבל זה לא נותן לך שום מידע שלא היה לך קודם. |
 |
 |
 |
|
 |
||
|
||||
 |
מדוע הידיעה לגבי מה שנמדד בצד השני לא נותן לך שום מידע שלא היה לך קודם ? |  |
 |
 |
|
 |
||
|
||||
 |
כאשר אתה רוצה להעביר מידע, אין כוונתך להעביר אוסף אקראי של סימנים (ולא משנה אם מדובא באותיות, בביטים של אפסים ואחדים, או בספינים של חיובי ושלילי), אלא אוסף סימנים המיצגים דבר מה. על מנת שתוכל לבצע טלפורטציה בעלת משמעות, עליך *לקבוע* את הספין של האלקטרון מצידו האחד של ה"קו", וע"י כך להכתיב את הספין של האלקטרון בצידו השני. כדי ליצור תקשורת,לא מספיק לדעת מה מתקבל בצד השני, צריך לגרום לכך. |
 |
 |
 |
|
 |
||
|
||||
 |
כאשר אמרתי טלפורטציה התכוונתי למה שאמרתי - העברת מידע באפס זמן. ואכן בניסוי עובר מידע באפס זמן - ואכן כך : לאלקטרון שלא נמדד אכן עובר המידע של איזה ספין הוא צריך להיות. כי המדידה קובעת בצורה אקראית את הספין של האלקטרון הנמדד, וכך קובעת גם את הספין של האלקטרון שלא נמדד (העברת מידע) - עקב המיידיות של המדידה זה קורה באפס זמן, לא משנה מה המרחק בין האלקטרונים. איך אפשר לנצל את קביעת הספין המיידית הזאת לצורכי תקשורת ו/או העברת חומר ביום-יום, זאת איני יודע. (הלוואי וכן). |
 |
 |
 |
|
 |
||
|
||||
 |
הלוואי שכן, אבל כל עוד חוקי הפיזיקה לא ישתנו, זה לא יקרה. לא ניתן (גם לא תאורטית) לנצל את קביעת כיוון הספין לצורך העברת מידע. אני גם לא ממהר להגדיר את קביעת הספין של האלקטרון השני כ''העברת מידע'' כי קשה לי לחשוב על אלקטרון כ''צרכן של מידע''. |
 |
 |
 |
|
 |
||
|
||||
 |
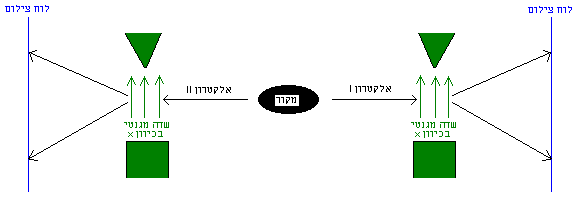
יהי א' מקור של אלקטרונים מצומדים הנורים לכיוונים מנוגדים. נניח שהם במצב סינגלטי - דהיינו בספינים הפוכים זל"ז. יהי ב' משדר האינפורמציה אותה אני רוצה לשדר לצד ג'. עתה עלי לתכנן קופסה (להלן: ד') שמקבלת את האינפורמציה מב' וסוכמת אותו עם האינפורמציה מא'. ד' יכולה להיות למשל שער XOR עם טבלת אמת כדלהלן: כניסה א' | כניסה ב'| מוצא ד' 0|0|0 1|0|1 0|1|1 1|1|0 את המוצא מד' אני מזין למשדר המכוון לעבר צד ג'. צד ג' מבצע מדידה של א' ובאמצעות זאת קובע *מיידית* כיצד לשערך את האינפורמציה ב' לפי הקלט ד'. יותר מכך, נניח שצד ג' מצויד במשחזר ה' המבצע פעולת XOR של הקלט ד' עם הקוד א': כניסה א' הפוכה* | כניסה ד'| מוצא ה' 0|0|0 1|1|0 0|1|1 1|0|1 לקחתי את כניסה א' בדיוק כפי שהופיעה בטבלה לעיל, ואת כניסה ד' בדיוק כפי שהתקבלה בטבלה לעיל. פעולת XOR בין שתיהן החזירה לי תוצאה ה' הזהה בדיוק לאינפורמציה ב' בטבלה לעיל. משמע - בלי למדוד את א', רק ע"י הזנת א' לפעולת XOR הן במשדר והן במקלט, הצלחתי לשחזר *במדויק* את האינפורמציה ב' על-פי קוד ששידרתי במהירות האור למשדר ד' ולמקלט ה' בצד ג'. מספיק טוב? * - כיוון שהנחתי שהאלקטרונים משוגרים בספינים מנוגדים למשדר ד' ולמקלט ה', על צד ג' לבצע פעולת XOR של התשדורת ד' עם *ההיפך* של הקלט מא'. כמובן שעבור אלקטרונים בספינים זהים לא הייתי צריך להפוך. |
 |
 |
 |
|
 |
||
|
||||
 |
אני בטוח שפספסתי משהו. אם הבנתי נכון, הרי שאתה למעשה "מצפין" את השדר (ב') על פי מפתח שמורכב מספינים שלא מדדת (א'). את התוצאה - (ד') אתה *משדר* לצד ג', ושם אתה מזין למפענח (ה'), שוב בלי למדוד ממש, את רצף הספינים בצד השני (א' תג) שמובטח שהוא הפוך. זה נותן לך בחזרה את השדר (ב'). עד כאן נכון? אנא אשר או הפרך. עכשיו, העניין הוא שאני לא מבין מה כל זה עזר לך. האלקטרונים "מחליטים" על הספין שלהם רק בעת מדידה. באיזו נקודה אתה מודד אותם, אם בכלל? האם הכוונה היא למדוד רק בצד ג', וכך לקבוע את המפתח? מה היתרון בזה? אתה בכל זאת צריך לשדר משהו מצד ב' לצד ג' בטכנולוגיה קיימת (שלוקחת זמן). אמנם את הספינים אתה מקבל מיידית, אבל אתה לא יכול לקבוע אותם מראש. מה שאתה כן קובע מראש אתה חייב לשדר באופן רגיל ואיטי - גם אם עשית עליו מניפולציות עם א'. מה הרווחנו כאן? |
 |
 |
 |
|
 |
||
|
||||
 |
לדעתי דווקא עקבת היטב אחרי התהליך. המקור א' משדר קוד אקראי לשני הצדדים. האינפורמציה ב' מוצפנת באמצעות הקוד א'. מתקבל שדר מוצפן ד' אותו מסוגל לפענח רק מי שמקבל את הקוד מא' בתיזמון המתאים. ראינו שאין צורך למדוד במפורש את א', די לבצע פעולת XOR נשנית בין השדר המוצפן ד' (שהוא בסה"כ א'XORב') לבין הקוד א'. דומני שאתה שואל את השאלה הפשוטה הבאה - איפה פה נכנס הקטע של העברת מידע באופן מיידי, ללא מגבלות מהירות האור. והתשובה הפשוטה היא - הוא לא נכנס, כל האינפורמציה (ד') שודרה במהירות האור. אך הקידוד הוא חסין לציטוטים ואמין ביותר. |
 |
 |
 |
|
 |
||
|
||||
 |
כל מה שאמרת נכון, אבל עדיין לא מאפשר מעבר של מידע בין שני אנשים (או מחשבים) במהירות שעולה על מהירות האור. (שעל זה דיברנו) למעשה העקרון של ''טלפורטציה'' מאפשר להעביר בעזרת מכונה דומה לשלך מספר מרוכב בכל דרגת דיוק רצויה ע''י שני ביטים (אלקטרונים במקרה הזה) בלבד. |
 |
 |
 |
|
 |
||
|
||||
 |
מי זה "המקור א"'? מה הקשר שלו להצפנה? האם מדובר בהצפנה תלת צדדית בה "סומכים" על א' שלא ירמה? תחשוב שאם אני יושב על הקו בין א' ל-ב' אני יכול לרמות אותו ולשלוח לו קוד שאני המצאתי במקום את מה ש- א' שלח ואז הוא "מצפין" את האינפורמציה שלו לפי קוד שאני מכיר ויכול לפענח בלי בעיה. שאלה נוספת, האם "השדר המוצפן ד"' הוא שדר קוואנטי וצריך "טלפון קוואנטי" כדי להעביר אותו? |
 |
 |
 |
|
 |
||
|
||||
 |
א' הוא כולה מקור האלקטרונים המצומדים שתיאר ירדן. אתה אמנם יכול לחבל בקו בין א' לב' כפי שהצעת, אלא אם א' הוא קופסה שחורה קטנה שיושבת בתוך המשדר ד'. השדר המוצפן ד' הוא שדר רגיל לכל דבר ועניין. אתה יכול לשדר אותו ברדיו, להקריא אותו בטלפון או לשלוח אותו על גבי יונות דואר. |
 |
 |
 |
|
 |
||
|
||||
 |
אבל אם א' יושב בתוך ד', איך האלקטרונים הצמודים (יש לי בעיה עם המונח הזה, צימוד זה coupling ולא entanglement שעדיין לא שמעתי תרגום ראוי לו בעברית) מגיעים למפענח? |  |
 |
 |
|
 |
||
|
||||
 |
entanglement - שזירה. מעתה אמור - אלקטרונים שזורים. |  |
 |
 |
|
 |
||
|
||||
 |
עפ"י האקדמיה ללשון העברית תרגום המילה entanglement הוא סבך. אמנם הביטוי מגיע ממילון הימאות, אבל נדמה לי שהביטוי הולם גם את הנושא המדובר. מעתה אמור - אלקטרונים סבוכים. דרך אגב, אפנה אתכם למנוע מצויין לחיפוש מונחים עבריים: http://hebrew-terms.huji.ac.il אני קורא לכל החברים להעדיף את השימוש במונחים עבריים. עכשיו תוכלו גם למצוא אותם ללא קושי. |
 |
 |
 |
|
 |
||
|
||||
 |
כאן נכנס הקטע המגוחך מעט בקונפיגורציה החדשה - ד' משדר לצד ג' גם את המסר המוצפן, וגם את הצופן א'. בשביל לשדר את הצופן א' צריך ''טלפון קוונטי'', או לפחות להתקין תחנת מדידה לא' ליד שובך יוני הדואר. ד' משודר כאמור בכל צורה ואופן העולים על דעתך. |  |
 |
 |
|
 |
||
|
||||
 |
ברור לך שזו בעיה: אתה משדר את המפתח שלך באויר ביחד עם המסר המקודד. זה לא בטוח במיוחד. |  |
 |
 |
|
 |
||
|
||||
 |
הטלפורטציה מתבטאת בכך שניתן להעביר במדויק את המצב הקוואנטי של גוף מסוים (להלן א') לגוף אחר (להלן ב') ובכך ''מבחינת היקום'' מה שהיה קודם גוף א' הוא כעת במדויק גוף ב' (המצב הקוואנטי של גוף א' נהרס תוך כדי כך, אפשר להוכיח תיאורטית שאי אפשר ''לשכפל'' מצב קוואנטי). על מנת לבצע את ההעתקה עדיין יש צורך בהעברת מידע ''אמיתי'' שלא יודעים (ולפי איינשטיין אי אפשר) להעביר במהירות נמוכה ממהירות האור. |
 |
 |
 |
|
 |
||
|
||||
 |
נניח שא' משגר רצף של אלקטרונים שזורים ל-ב'. ב' עורך את המדידות שלו ומקבל ברבע מהן את הספין "UP". בשלב מסוים, א' מתחיל לערוך את המדידה על האלקטרונים שאצלו, ומאותו רגע הההסתברות ש-ב' מקבל הופכת להיות משהו מעל שליש. עבר, אם כן, לפחות ביט אחד של אינפורמציה ("א התחיל למדוד")1 באפס זמן או, ליתר דיוק, בפרק הזמן שלוקח לב' לבצע מספיק מדידות כדי להשתכנע שההסתברות אכן השתנתה. מאחר והמרחק בין א' לב' אינו מוגבל, פרק הזמן הזה יכול להיות קטן ככל שנרצה יחסית למרחק, כלומר מהירות המעבר התיאורטית גדולה כרצוננו. אני יודע שאני טועה, אבל לא יודע איפה. ------------- 1 אולי אפשר לטעון שלא רק ביט אחד, הרי גם שעת תחילת המדידה "עוברת" ל-ב', אבל זה פחות חשוב להבנתי כרגע. |
 |
 |
 |
|
 |
||
|
||||
 |
המודד המכונה ב' יקבל חצי מהאלקטרונים במצב ספין למעלה. ברבע מהמקרים זה יהיה זהה למדידה של א', שגם כן מקבל חצי במצב ספין למעלה. כפי שהוסבר, המודד א' לא יכול בשום דרך להעביר מידע אל המודד ב' באפס זמן. (גם אם האלקטרונים עצמם יכולים) |
 |
 |
 |
|
 |
||
|
||||
 |
אני רואה שהתגובות פה ישנות מאוד, אבל אולי יהיה לי מזל ומישהו שיודע ייתקל בשאלה. לא הבנתי איך התגובה שלך פותרת את השאלה המקורית, אז אני אציג מצב שנראה לי ברור יותר: משתמשים במקור המייצר זוגות אלקטרונים שזורים בעלי מצב ספין סימטרי. מעבירים מיד את שני האלקטרונים דרך מודד ספין Y ומעבירים הלאה רק את אלה שספינם מעלה. כעת האלקטרונים נשלחים אל מקלטים רחוקים, א' וב'. ב-ב' הם כולם מועברים דרך מודד ספין Y (ונמדד ספין Y מעלה?), ובא' הם מועברים דרך מודד ספין X שאיננו פועל (זה מצב 0) כעת רוצים לשנות את האות ל-1, מפעילים את מודד הספין X ב-א', וכעת האלקטרון ב-ב' נמצא בסופר פוזיציה של ספין Y מעלה וספין Y מטה (לפי אי הוודאות), מה שניתן לראות במדידה בב'. כעת אפשרי לראות שהועבר אות 1 במקום אפס והועבר מידע מהר ממהירות האור. השאלה שבאה כעת, האם השגיאה כאן היא ההנחה שהאלקטרונים נשארים במצב ספין Y מעלה לאחר שהתרחקו מהמדידה הראשונית? אם כן, האם הדעיכה (מהמצב המדוד) שלהם מביאה אותם לסופרפוזיציה שוב מהר כל כך שלא ניתן למדוד מעבר מידע המהיר ממהירות האור? ייתכן שההסבר לכך דורש ידע נוסף? או שפספסתי שגיאה אחרת, פשוטה יותר. |
 |
 |
 |
|
 |
||
|
||||
 |
פספסת משהו קטן - מדידה של הספין בכיוון כלשהו גורמת מיד לקריסה של המצב השזור למצב לא שזור (סימטרי או א-סימטרי לפי המצב המקורי, שים לב שלא ניתן ליצור מצב שזור סימטרי בו זמנית בכל כיווני הספין). בהנחה שהמצב המקורי היה סימטרי בכיוון Y, אחרי המדידה תקבל מצב לא שזור של זוג אלקטרונים במצב ספין למעלה בכיוון Y. כעת לא משנה מה תעשה לאלקטרון אחד, השני ישאר באותו מצב, כלומר ב׳ ימדוד תמיד ספין למעלה בכיוון Y. |  |
 |
 |
|
 |
||
|
||||
 |
אוקיי, תודה רבה על התשובה, אבל זה עדיין לא עונה לי על כל השאלות, או לפחות לא סוגר לגמרי את החשד שלי שכן אפשר להעביר מידע. השאלה עכשיו שלי היא כזאת: האם ניתן למצוא מקור שפולט אלקטרונים שזורים שהסופרפוזיציה שלהם ביחס לציר כלשהו היא לא חצי-חצי, כלומר לקבל אלקטרונים שזורים שהחלוקה שלהם בתוך מודד ספין בכיוון ידוע מראש כלשהו לא מתכנסת לחצי-חצי? אם לא, אז נגמרו לי הרעיונות ואני שמח שסגרנו את הנושא, אם כן אז נראה לי שאפשר להוציא מזה העברת מידע מהר יותר ממהירות האור (אם כל היוצא מזה). |  |
 |
 |
|
 |
||
|
||||
 |
ניתן ליצור מצב של שני אלקטרונים עם פרמטר שזירה t כך שההסתברות לקבל את שני האלקטרונים במצב ספין מסויים עבור ציר מסויים (למשל שניהם למעלה או אחד למעלה והשני למטה) הוא t וההסתברות לקבל את המצב ההפוך (בדוגמאות הנ״ל שניהם למטה או הראשון למטה והשני למעלה בהתאמה) בהסתברות 1 פחות t. גם זה לא מאפשר לך להעביר אינפורמציה במהירות שעולה על מהירות האור. |
 |
 |
 |
|
 |
||
|
||||
 |
אני תוהה בקשר להיתכנות המצב הסימטרי לפי הגדרתך. משפט הספין-סטטיסטיקה לא אומר שזוג אלקטרונים אמור להימצא תמיד במצב אנטי-סימטרי? (כמובן שבתור ניסוי מחשבתי אפשר להשתמש בפוטונים במקום, אבל עדיין אשמח לשמוע באשר לאלקטרונים.) |  |
 |
 |
|
 |
||
|
||||
 |
אין לי מושג בפיזיקה ישומית, אבל היפותטית ניתן ליצור זוג אלקטרונים במצב אנטי-סימטרי ואז להפעיל על אחד מהם אופרטור היפוך פאזה והיפוך ספין (אופרטור פאולי Y) ולקבל מצב סימטרי. למיטב ידיעתי אופרטורים כאלו ניתנים למימוש. |  |
 |
 |
|
 |
||
|
||||
 |
האם הם מקיימים עדיין את עקרון האיסור גם לאחר שמצב של שתהין נקבע? |  |
 |
 |
|
 |
||
|
||||
 |
איזה עקרון איסור? של פאולי? בוודאי! |  |
 |
 |
|
 |
||
|
||||
 |
האם תורת הקוונטים מתעסקת אך ורק בנבואת כיוון אלקטרונים? איך אפשר לישם דברים כאלה? כבר שני מאמרים עוסקים בכיוונים זויות וסטטיסטיקה |
 |
 |
 |
|
 |
||
|
||||
 |
תורת הקוונטים, כשלעצמה, מהיותה תורה פיזיקלית, מתעסקת אך ורק בנבואת כיוון אלקטרונים, זוויות וסטטיסטיקה (וכיוצא באלה). ואני בכלל לא באתי לתאר את כל תורת הקוונטים או רק את תורת הקוונטים; באתי להציג בעיה ספציפית (בחלק הבא). בדרך לשם, אכן, היה עלי להציג כמה היבטים חשובים של תורת הקוונטים (כמובן שברובד אחר, זו היתה אחת המטרות של סדרת המאמרים). יש ישומים לתורת הקוונטים, אבל הם יאלצו להמתין למאמר אחר (ולכותב אחר, יש להניח). |
 |
 |
 |
|
 |
||
|
||||
 |
וקצת להרחיב על דבריו של ירדן. תורת הקוונטים מתעסקת בחלקיקים קטנים, אטומים ומטה. (אולי טיפה במולקולות פשוטות) כשעובדים בקנה מידה כזה, הדברים היחידים שרלוונטים הם המיקום (כולל זמן) והתנע (כולל אנרגיה) ומתברר שיש גם תכונה נוספת שנקראת "ספין". כל שאר הדברים לא רלוונטים או לא ניתנים למדידה. מתברר, שכמעט כל התכונות של החומרים השונים (צבע, ברק, מוליכות חשמל/חום, פעילות כימית וכד') תלויות בהתנהגות של האלקטרונים בחומר, וזו בתורה מוסברת ע"י תורת הקוונטים. |
 |
 |
 |
|
 |
||
|
||||
 |
> תורת הקוונטים מתעסקת בחלקיקים קטנים, אטומים ומטה. > (אולי טיפה במולקולות פשוטות) מולקולה של 70 אטומי פחמן (fullerene C70) זה כבר חלקיק לא כל כך קטן. |
 |
 |
 |
|
 |
||
|
||||
 |
תודה על ההפניה. הניסוי למעשה רק מדגים את עקרון דה-ברוי (De-Broglie) שהוא נכון לכל גוף בכל גודל בתנאי שהוא נע מספיק מהר. ההשג המשמעותי כאן הוא עצם היכולת להבחין באפקט קוונטי בהתנהגות של מולקולה גדולה, אבל לפי דב-ברוי, האפקט קיים גם בכדורי טניס, רק שאנחנו (עדיין?) לא מסוגלים למדוד אותו. לפי המאמר, אורך הגל של המולקולות C70 הוא מספר פיקומטרים (מאית של אנגסטרם) כלומר זניח לחלוטין ביחס לגודל המולקולה עצמה, מה שרומז שלתוצאה לא יהיו השלכות ישומיות על השימוש במולקולה. עדיין יהיה ניתן לקבוע את המיקום שלה ואת התנע שלה בדיוק גבוה כרצוננו ללא התחשבות בעקרון אי הודאות. בכל מקרה, מדובר בהישג מרשים, שמדגים את תקפות תורת הקוונטים בעולם המקרוסקופי. |
 |
 |
 |
|
 |
||
|
||||
 |
האם הוסבר (ופיספסתי) למה התחזית של תורת הקוונטים היא לרבע תוצאות שוות כיוון? ואם לא אז למה? |
 |
 |
 |
|
 |
||
|
||||
 |
בחלק א' סיפרנו שלאקטרון שפונקציית הגל שלו היא ספין-X 'מעלה', יש סיכוי של רבע לצאת 'מעלה' במדידת ספין בכיוון 120 מעלות ביחס לכיוון X (ובאחת התגובות צוין שהפוקנציה היא ריבוע הקוסינוס של חצי הזווית). בחלק זה הרחבנו זאת, למצב של שני אלקטרונים מצומדים1 שפונקציית הגל שלהם היא אחת ומצבם זהה. אם בצד אחד אנו מודדים כיוון A, ובצד השני כיוון B, יחס התוצאות יהיה כאילו מדדנו לאותו אלקטרון A ואחר כך B. 1 במינוח של המאמר, שהוא אולי בעייתי. מישהו כאן הציע "שזורים". |
 |
 |
 |
|
 |
||
|
||||
 |
ואולי כדאי להוסיף שזו לא רק התחזית של תורת הקוואנטים - הטבע, בשבתו כבית המשפט הגבוה למציאות, מאשר את המספר הזה בניסוי. |  |
 |
 |
|
 |
||
|
||||
 |
כבר חששתי שלא יהיה לי מה לתרום לדיון הזה, ואז מה אני אוכל לומר להגנתי כשאיזה "אלמוני לרגע", ישאל מה אני עשיתי בשביל מדינה? שפעם עשיתי בגרות בפיזיקה 5 יחידות וקיבלתי בערך 80 נקודות יותר ממה שהגיע לי? שפעם ניסיתי לקרוא את "קיצור תולדות הזמן", וקפצתי על ההזדמנות הראשונה שבא איזה מישהו, שאינו בר סמכא בעליל, אמר לי שבדיוק בקטע הזה שבו אני נמצא עכשיו (בטח עמוד 50 או משהו, אני חושב שבאמת היה כתוב שמה כל מיני דברים על חצאי ורבעי ספינים, אבל אני לא מוכן להישבע על זה) כולם תמיד נשברים? בסוף מצאתי את זה (במקור על נייר אבל גיליתי שיש גם ברשת). אני לא יכול להגיד שזה שיעשע אותי במיוחד, ובדרך כלל בשעות האלה של הלילה אני עלול לצחוק אפילו מן ההומור הדק והשנון של דניאל קלטי (או אם תרצו "קארל גוסטב"), אבל מי יודע, אולי פספסתי כאן משהו: http://idi-web.idi.org.il/hebrew/article.php/?id=626 חוץ מזה, אולי איזה מישהו עם מקורות בבראנז'ה (או לפחות מישהו שמכיר שמות של מחזאים) יגיד לנו מי מסתתר מאחורי הפסבדונים "רשף ורגב לוי"? |
 |
 |
 |
|
 |
||
|
||||
 |
 |
 |
 |
|
 |
||
|
||||
 |
קארל גוסטב לא ממש מזכיר את קלטי. הוא דווקא מזכיר מישהו אחר. |  |
 |
 |
|
 |
||
|
||||
 |
 |
 |
 |
|
 |
||
|
||||
 |
את שכ''ג. ציפיתי ממך ליותר, למען האמת. |  |
 |
 |
|
 |
||
|
||||
 |
ניתוח טכסטואלי אינו תומך בהשערה שלך. |  |
 |
 |
|
 |
||
|
||||
 |
 |
 |
 |
|
 |
||
|
||||
 |
 |
 |
 |
|
 |
||
|
||||
 |
אחרי קריאת תגובה 107582 אני חוזר בי. קלטי. |  |
 |
 |
|
 |
||
|
||||
 |
תגובה 107582 אינה מייצגת את סגנונו של קרל שהוא אדם משכיל ובד"כ כתיבתו רהוטה. רוצה לומר : לא הסופר האדום. |  |
 |
 |
|
 |
||
|
||||
 |
קארל גוסטב הוא קלטי, במאה אחוז. אי אפשר לטעות בו. |
 |
 |
 |
|
 |
||
|
||||
 |
הוא אדם אמיתי ולא פסוודונים של אייל מוכר? יש לי תחושה חזקה שהאייל הוא קוואנטי - הוא מאפשר לאדם להיות שני מגיבים בעת ובעונה אחת. מצד שני זה מעלה את השאלה האם שני אנשים יכולים להיות מגיב אחד. רוצה לומר: עד שלא מדדנו בוודאות, קארל גוסטב הוא סופרפוזיציה של שכ"ג וקלטי. |
 |
 |
 |
|
 |
||
|
||||
 |
לרוע המזל, שכ"ג קרס (זמנית) ל"האייל המלנקק". האם הקריסה הזו גורמת לכל המערכת לקרוס? |  |
 |
 |
|
 |
||
|
||||
 |
בדיוק ההיפך, הקריסה ההיא מונעת את קריסת האייל. כדי להבין העניין צריך להעזר בתורת המי(ו)תרים, אבל לא כדאי להרגיז את יואל, או שהוא יתחיל לקלל. |  |
 |
 |
|
 |
||
|
||||
 |
סחתיין על ההשוואה של שכ''ג, שעם כל השטויות היה אחד האנשים האינטיליגנטים ביותר כאן, לשירי מירי, שחיינו היו חיים גם בלעדיה. |  |
 |
 |
|
 |
||
|
||||
 |
לקרוא בקול גדול למיץ פטל: אמא ואבא מודאגים מאד. הכל נסלח, שוב הביתה. באהבה, משפחת אייל. |
 |
 |
 |
|
 |
||
|
||||
 |
כן רבותיי, השוונג1 נמשך, כפי שניתן לראות כאן: תגובה 108013 (ולא שלא היו כאלה שדווקא כן ניסו לעצור אותי). ואפרופו שוונגים, הרשו לי לנצל את הבמה ולקרוא ל"אייל האלמוני והארסי" - חזור הביתה!2. <שיחה אישית בטלה, מיועדת רק לאייל האוא"ר, קוראים אחרים מתבקשים לדלג3> כמו שאתה יכול ללמוד מן הכותרת, סוף כל סוף קיבלתי את "בציר טוב", ולמי אני אספר על זה אם לא לך? ואת ההודעה הזאת שלך(?) (תגובה 106774) אני קורא כל לילה לפני השינה, ובכלל, אם הייתי מכיר שירי משוררים כבר מזמן הייתי מקדיש לך אחד. <סוף שיחה אישית בטלה וגו'. עדיין לא חייבים לקרוא>. --------------------------------------------------- 1תגובה 103183 2כן, שמתי לב שהקריאות האלה עכשיו באופנה ב"אייל". 3מה אני אעשה, אין לו מייל. |
 |
 |
 |
|
 |
||
|
||||
 |
על מה אתם מדברים במקום הזה? יש פה איילים ארסיים? אמאל'ה... אני מפחדת. אין לי מושג לאן שלחתם אותי. ואיך זה קשור לפיזיקה? |
 |
 |
 |
|
 |
||
|
||||
 |
מי כמוך יודע. |  |
 |
 |
|
 |
||
|
||||
 |
איילים ארסיים זה ביולוגיה. אבל אני לא חושבת שיש כאלה בכלל. וזה לא נראה לי קשור לבעיית המדידה. |
 |
 |
 |
|
 |
||
|
||||
 |
תגידי, הצלחת לבנות שער טופולי נורמלי משערי פרדקין? בחייאת, קשה לאללה. |  |
 |
 |
|
 |
||
|
||||
 |
לא כל דבר זה פסבדונים, גם אם אתה מדור האיקס. יש פה סיפור אמיתי לגמרי ואף עצוב - מדובר בזוג אחים צעירים שכתבו ופרסמו יחד, בחתימה משותפת. לאחר שאחד מהם נפטר (לא זוכרת באיזה נסיבות), האח השני ממשיך לפרסם בשם המשותף. |
 |
 |
 |
|
 |
||
|
||||
 |
אמת. היה על זה כתבה ב''העיר'' לפני מספר חודשים. |  |
 |
 |
|
 |
||
|
||||
 |
(ציטוט מתוך המאמר אליו קישרתי, ואותו ברקת לא קראה עד הסוף) אולי לא כל דבר זה פסבדונים, אולי אני מדור האיקס ואולי באמת מדובר כאן על סיפור אמיתי (ובאמת כשדיברתי על מישהו עם מקורות בבראנז'ה2 הייתה לי בראש רק כותבת אחת כאן, כי הגיקים האלה מה הם כבר יודעים מהחיים שלהם), אבל את התלונות האלה את צריכה להפנות לחבר'ה מ"העין השביעית". 1היי טל, סידרת שאפשר יהיה לכתוב כותרות ארוכות? זה בעקבות הבקשה שלי? תודה! 2שמבחינתי זה כמעט כל אדם עם גישה סדירה ל"העיר". |
 |
 |
 |
|
 |
||
|
||||
 |
פיטים. בראנז'ה = כל מי שקונה עיתון בשביל לראות אם החברים שלו כתבו הפעם. מזלי שאני קוראת עיתונים (כמעט) רק ברשת. |
 |
 |
 |
|
 |
||
|
||||
 |
מה הבעיה פה? השם האמיתי של התסריטאי והמחזאי הוא רשף/רגב לוי, זה עדיין פסבדונים. וחוץ מזה - תודה על הקישור העקיף לגליון החדש של העין השביעית. (פה: http://idi-web.idi.org.il/hebrew/article.php?id=6ef6...) אני כבר חודשים מנסה להבין מה קרה להם, כי אני כל הזמן בדקתי כאן: ולא היו שום עדכונים. |
 |
 |
 |
|
 |
||
|
||||
 |
והלא כתוב לך שם בפירוש, באותיות רבתי - OLD ! :-) |
 |
 |
 |
|
 |
||
|
||||
 |
לא הבנתי - איך שם אמיתי יכול להיות פסבדונים? |  |
 |
 |
|
 |
||
|
||||
 |
הפסבדונים הוא השילוב של השמות של שניהם, מכיוון שאחד מהם כבר איננו בין החיים. ברגע שהשם מפסיק לייצג יישות שקיימת במציאות, הרי שהוא הופך לפסבדונים. |
 |
 |
 |
|
 |
||
|
||||
 |
מישהו מוכן להסביר לי, איך הגענו מטלפורטציה לשמות פסבדונים.... 2) ומה קרה בסוף לחתול של שרדינגר? |
 |
 |
 |
|
 |
||
|
||||
 |
בניסוי שולחים זוג אלקטרונים מצומדים לשני כיוונים. אם מודדים לשניהם את ספין-x, מקבלים אותה תוצאה. נניח שאחר-כך מודדים לשניהם גם את ספין-y - האם התוצאות עכשיו הן בלתי תלויות? |  |
 |
 |
|
 |
||
|
||||
 |
מכניקת הקוונטים אומרת שריק (ווקום) מוחלט לא יכול להתקיים, למה? |  |
 |
 |
|
 |
||
|
||||
 |
בגלל עקרון אי הוודאות. איך זה קשור? העקרון אומר שתמיד יש אי ודאות, למשל בקשר לאנרגיה. כלומר, יתכן שבואקום מוחלט תופיע פתאום, יש מאין אנרגיה, שממנה יווצרו חלקיקים, וזאת בתנאי שהמכפלה של האנרגיה הכוללת כפול זמן הקיום תהיה קטנה מאוד. כמה קטנה? מאוד מאוד קטנה. כמו כן חייבים להתקיים חוקי השימור - תנע, תנע זוויתי, מטען, ומספרים קוונטים נוספים. |
 |
 |
 |
|
 |
||
|
||||
 |
כן. למה? כי מדידה של מערכת עם צימוד הורסת את הצימוד. |
 |
 |
 |
|
 |
||
|
||||
 |
קראו כאן שמהתיאוריות הנ"ל נובע שה' מנהל את העולם ב"זמן אמת", עד רמת האלקטרון הבודד: |
 |
 |
 |
|
 |
||
|
||||
 |
הכיוון של השדה המגנטי- X הוא קבוע או משתנה ? אני כמעט בטוח שזה משתנה אחרת אין שום סתירה באי שיוויון בל לEPR ... |
 |
 |
 |
|
 |
||
|
||||
 |
לא בטוח שהבנתי את השאלה. מה נחשב "כיוון X" נקבע שרירותית, אבל קבוע במשך הניסוי. |  |
 |
 |
|
 |
||
|
||||
 |
לא ברורה לי הסתירה בין אי השיוויון של בל למסקנה של EPR לגבי המשתנים החבויים שהרי איננו יודעים את טיבם של המשתנים הללו ןלכן ניתן להניח שההשפעה שלהם על ההסתברות מעלה\מטה של האלקטרונים שונה בכיוון של למעלה מ120 מעלות מX. מה אני מפספס פה? |
 |
 |
 |
|
 |
||
|
||||
 |
צר לי, אני לא מבין את האי-הבנה. במאמר יש הסבר מאוד מפורט; התוכל לומר לי היכן בהסבר בדיוק אתה מפסיק להשתכנע? |  |
 |
 |
|
 |
||
|
||||
 |
המדידה של צד ימין השפיעה על התוצאות של צד שמאל(או ההיפך)... למה לא עשו ניסוי כשבצד אחד A ובצד שני B ואז היו רק רבע מהתוצאות זהות והיינו מגיעים לאותה המסקנה ....? |
 |
 |
 |
|
 |
||
|
||||
 |
התגובות שלך קצרות מדי ומרומזות מדי. אני עדיין לא מבין. המשפט הראשון שלך הוא - ציטוט מהמאמר? הצעה לפתרון? בניסוי שמתואר במאמר, חלק מהמדידות הוא כן בצד אחד A ובצד שני B - זה חלק מהטיעון. שוב - התוכל להצביע על משפט מסוים במאמר, ולומר - המשפט הזה, בהקשר הזה, נראה לא ברור או לא משכנע? |
 |
 |
 |
|
 |
||
|
||||
 |
קודם כל, אחרי ההסבר שלך אני חושב שאני מבין את המאמר ואת המסקנה שאין משתנים חבויים ושתוצאת המדידה בצד שמאל משפיעה על התוצאה בצד ימין,אם הבנתי נכון זאת הנקודה של המאמר... עכשיו אני חושב על ניסוי שנראה לי פשוט יותר אולי מתוך חוסר הבנה, כך אני רואה את הניסוי הפשוט והברור יותר- מהמקור יוצאים שני אלקטרונים צמודים אחד ימינה ואחד שמאלה בצד ימין ספיןA(אני לוקח את הכיוונים A וB מאי שיוויון בל) בצד שמאל ספין B - נקבל רק ברבע מהתוצאות מעלה\מעלה או מטה\מטה מה שיוכיח סטטיסטית שאין משתנים חבויים לא? |
 |
 |
 |
|
 |
||
|
||||
 |
לא - זה כבר כמו EPR. נניח שיש לנו שני משתנים חבויים "שקל" ו"לירה", שלכל אחד מהם ערכים אפשריים "עץ" ו"פלי" בהתפלגות חצי-חצי. "שקל" קובע את תוצאת מדידת ספין A, ו"דולר" את תוצאת ספין B. שני הגדלים זהים בין שני האלקטרונים בכל זוג. אם השקל והלירה הם בלתי תלויים, אז הם יהיו שונים בהסתברות חצי וזהים בהסתברות חצי, ואז ההסתברות לתוצאה זהה במדידת ספינים היא חצי - זה אולי מה שמבלבל כאן. הטריק הוא שהם לא חייבים להיות בלתי-תלויים: התיאוריה יכולה להיות כזו שכש"שקל" הוא עץ, אז "דולר" הוא עץ ב-3/4 מהאלקטרונים ופלי רק ברבע, ולהפך. ואז זה מסתדר (ואפילו באופן טריוויאלי) עם סטטיסטיקת הניבויים. וזה גם לא מופרך: התוצאה החזויה של רבע-שלושה רבעים מתקבלת מנוסחה מתמטית פשוטה (ריבוע הקוסינוס של חצי הזווית, אם אני זוכר נכון); אז אין בעיה "להנדס" משתנה חבוי שיתנהג מראש לפי נוסחה כזו. |  |
 |
 |
|
 |
||
|
||||
 |
יש לי בעיה עם זה וכמו שאני מבין את זה כרגע וגם חשבתי מקודם ניסוי EPR סותר את המסקנות שלו עצמו... מה שרשמת עם ה"שקל" וה"דולר" מחדד את זה יפה מאוד ואני לוקח את זה חזרה לניסוי EPR המקורי - אם אנחנו בודקים ספיןB בשני הצדדים(במקום X בניסוי המקורי B - אין הבדל) הרי שאנו מניחים שגם כאן "שקל" ו"דולר" נמצאים ויוצרים עבור B הסתברות של רבע - שלושה רבעים כי הרי המסקנה של EPR היא שאין תלות בין שני האלקטרונים אחרי שהם נפרדים ולא משנה שהחלפנו את A בB באחד הצדדים! למרות זאת התוצאות יראו הסתברות של חצי ששונה מרבע-שלושה רבעים בניסוי שלנו . זה לא בעייתי מבחינת EPR....? עדיין לא מסתדר לי... |
 |
 |
 |
|
 |
||
|
||||
 |
גם ב-EPR ההסתברות (עפ"י תורת הקוונטים) תהיה רבע-שלושה רבעים אם המדידות בשני הצדדים הם בזווית של 120 מעלות. חצי-חצי זה בזווית של תשעים מעלות. או שלא הבנתי את הטענה? (עכשיו אני נוסע לשבוע - המשך יבוא, מן הסתם.) |
 |
 |
 |
|
 |
||
|
||||
 |
לכן שאלתי בתגובה הראשונה אם X משתנה... אם X משתנה בניסוי EPR אז X=B והתוצאות החזויות אינן רבע-שלושה רבעים אלא חצי-חצי... דרך אגב כך גם אני מבין גם את הניסוי המקורי מחלק א' ואת אי שיוויון בל שם A, B וC יכולים להשתנות בכל ניסוי אך היחס בינהם נשמר... אז עכשיו אני אמור להבין שA הוא קבוע? וגם X בכל שאר הניסויים?... אז זהו, תודה על השיחה המעניינת, עד הפעם הבאה. |
 |
 |
 |
|
 |
||
|
||||
 |
x הוא (כמובן) שרירותי בניסוי; צריך (כמובן) שהוא יהיה תואם בשני הצדדים. האם אפשר לשנות אותו בין זוג לזוג? נראה לי שכן, ושזה לא משנה לטיעון (של EPR או של בל); הרי אין בטיעונים תלות בין זוג לזוג, רק תוצאות סטטיסטיות על התלויות בין בני זוג. |  |
 |
 |
|
 |
||
|
||||
 |
אם X שרירותי אז בEPR הוא יהיה 120 מעלות משני הצדדים ובכל זאת התוצאה תהיה זהה ... כלומר 50% מעלה-מטה, לא? אצל בל הרעיון הוא שבכל צד יש לך זוית שונה - ואז באה לידי ביטוי התופעה של רבע-שלושה רבעים - רשמתי מקודם ניסוי שהמחיש את התופעה הזו, אלא אם כן לא הבנתי משהו... |
 |
 |
 |
|
 |
||
|
||||
 |
למה אתה מתכוון ב"120 מעלות משני הצדדים"? ציון המעלות בהסבר שלי מתייחס תמיד להפרש בין שני הצדדים - אין "זווית אבסולוטית". אם ההפרש בין הצדדים הוא 120 מעלות, אז התוצאה תהיה 1/4-3/4. |  |
 |
 |
|
 |
||
|
||||
 |
כשאני מודד 90 מעלות אני מקבל בצד שמאל 50% מעלה כשאני משנה ל120 מעלות(ע"י שינוי כיוון השדה המגנטי בצד ימין) אני מקבל בצד שמאל יחס שונה, לא הבנתי איך זה מסתדר עם EPR, הרי המשתנים החבויים לא השתנו, שום דבר לא השתנה בניסוי מלבד מה שנמדד בצד האחר! וזה הרבה יותר פשוט מאי שיוויון בל,לא? |
 |
 |
 |
|
 |
||
|
||||
 |
(מצטער על האיחור בתשובה) אתה אומר משהו כזה, אם אני מבין נכון: נניח שאנחנו משגרים זוג. בצד שמאל אנו מודדים ספין בכיוון קבוע A. בצד ימין אנחנו יכולים למדוד B או C. כיוון B הוא 90 מעלות ל-A, כיוון C הוא 120 מעלות ל-A. רק אחרי השיגור אנחנו בוחרים מה למדוד בצד ימין. אז אנחנו עושים סטטיסטיקה, ורואים שכשמדדנו B, היתה התאמה חצי (בחצי מהזוגות יצאה תוצאה זהה), וכשמדדנו C היתה התאמה רבע. האם זה מסתדר עם משתנים חבויים? כן, זה מסתדר בקלות. קח משתנה חבוי שזהה בין בני הזוג, קבוע מרגע השיגור עד המדידה, נותן חצי-חצי באופן אקראי לתוצאות "מעלה"-"מטה" בכל כיוון, ומשתנה (מבחינת ההתסברות ל"מעלה") בהתאם לריבוע הקוסינוס של חצי הזווית (כלומר, בשינוי כיוון של 90 מעלות הוא מחליף דגל (בין "מעלה" ל"מטה") בהסתברות חצי, ובשינוי כיוון של 120 מעלות הוא מחליף דגל בהסתברות שלושה רבעים). כפי שאתה רואה, למרות ששינוי כיוון המדידה באחד הצדדים נותן סטטיסטיקה שונה, הוא לא באמת מצריך שמשהו בצד השני ידע על כך. |
 |
 |
| חזרה לעמוד הראשי |  |
| מערכת האייל הקורא אינה אחראית לתוכן תגובות שנכתבו בידי קוראים | |
 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
|
© כל הזכויות שמורות |